★ Gとリンの数学夜話 ・ 第3回:かけると回る複素数 ★
2009/09/01
 |
 |
 |
「ふぇーん、、、」
「どうした、マスター。何かあったのか?」
「G、あたしって、数学の才能が無いのかなぁ。」
「マスター、それはあまりにも短絡的な思考だ。
問題が解けるかどうかと、頭の善し悪しは別のこと。
ましてや才能の有無など、全く関係ない。」
「・・・でもね、でもね、三次方程式っていうのが、全然わかんないんだよー。」
「マスター・・・」
Gは、ため息を漏らした。
「常識的に考えて、“三次方程式がわからないから、才能がありません”って言うやつがあるか?
マスターに足りないものは才能ではない、努力だ!」
「ほへっ?!」
「何の努力も無しに、一度聞いただけで解ろうっていうのが虫が良すぎる。
1に努力、2に努力。特にマスターには、基礎訓練が圧倒的に不足している!」
ががーん、そんなぁ・・・慰めてもらえるのを期待していたのになぁ。
そんな私の思いをよそに、Gはビシビシと続けた。
「方程式を解ろうというのなら、まずは複素数の知識が不可欠だ。」
そう言って、Gはやおら複素平面の図を描き始めた。
「また複素数ぅ、、、今日はそんな気分じゃないんだよなぁー。。。」
「何か言ったか?」
「いえ、何も!!」
とほほ、今日は最悪の日だ。。。
「まずは足し算からだ。
複素数の足し算を、この複素平面の図の上に書いたら、どうなる?」
「あのぅ、さすがに足し算は、もういいと思うんですけど。。。」
Gは無言でジロッっと睨んだ。
「・・・わかったよ、やればいいんでしょ、やれば。」
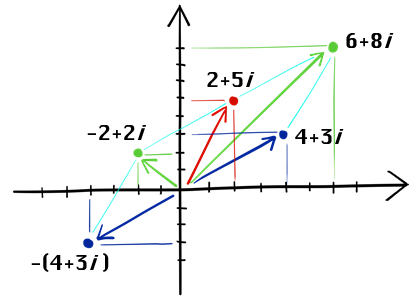
「その通りだ。例えば、(2+5i) + (4+3i) は?」
私はしぶしぶグラフの上にプロットした。
実数同士、虚数同士、足し算すればいいんだから、答は 6 + 8i 。
「次は引き算。(2+5i) - (4+3i) は?」
これも実数同士、虚数同士、計算すればいいんだね。答は -2 + 2i 。
「できた。」
「うむ、上出来だ。それで、図を見て何か気付いたことはないか。」
「えーっと、特に変わったところは無いように思うけど。。。」
「原点から、複素数の点までを、矢印で結んでみてごらん。」
矢印ねぇ、矢印っと、キュッキュ。
「この矢印をよく見てごらん。
足し算の矢印の先端同士を線で結んでみると・・・」
そう言いながら、Gは線を付け加えた。
「平行四辺形になる。
つまり、複素数の足し算は、ベクトルの合成なのだと考えればイメージしやすい。」
「なるほろー、ベクトルね。じゃ、引き算は?」
「引き算は、反対向きのベクトルの足し算だ。」
確かに、ベクトルを反転させてみると、平行四辺形ができた。
「さて、ここからが本番だ。複素数の掛け算。
例えば (1+i)・(-1-i) は?」
えーっと、1つづつ展開すればいいんだよね。
(1+i)・(-1+i)
= 1・(-1+i) + i・(-1+i)
= -1 +i -i -1
= - 2
「でーきた。」
「その通りだ。これも複素平面の上に描いてみよう。」
私は図の上に、3つの矢印を描いてみた。
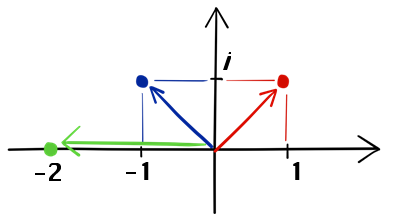
でも、例が1つだけだと、まず気付かないだろう。」
うーん、私は3つの矢印をじぃーっと見たけど、よくわからない。
「もっと良い例がある。
2乗したら i になる数、“リンの虚虚数”だ。」
「えーっ、なんでそんなこと覚えてるのよっ!」
まったく、恥ずかしー。
「褒めているのだぞ。
2乗したら i になる数、というのは、この複素平面上のどの辺りにあると思う?」
「えーと、えーと、、、1 と i の間あたり、かな?」
「良い勘をしているな。2乗してi になる数は (1/√2 + 1/√2i) 、1/√2 は約 0.7 だ。
この点を複素平面上に書いてみよう。」
0.7 ってことは、1 と i のちょうど真ん中というより、少し外側にふくらんだ位置にある。
「 i を2乗したら -1、この (1/√2 + 1/√2i) を2乗したら i 。
この絵を見て、気付くことは?」
「・・・なんか、円になってるっていう気がする。」
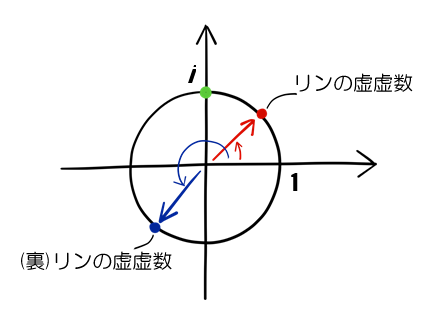
「ご名答! 1, i, -1, (1/√2 + 1/√2i) は、全て半径1の円周上に乗っている。
これが複素数の掛け算の謎を解く、最大のヒントだ。」
Gは図の上に、大きく円を描いた。
「それがわかんないから、苦労してるんじゃない。」
「では、1回掛け算したら -1 になる、ということだったらどうかな。」
「それなら * -1 ってことだよね。」
「 * -1 の意味を、図に描いたら?」
「えっと、反対向きってことかな。」
「そう、数直線の上で、180度反対向きになることだ。
だから、(-1) * (-1) は、反対の反対でプラスに戻る。
数というものを、ベクトルだと思えばわかりやすい。」
反対の反対は賛成、裏の裏は表、だから(-1) * (-1) = (+1) ってことでいいよね。
「そこでだ、もし * -1 が180度反対向きなのだとしたら、その半分は、何になる?」
「ええと、90度横向き、、、って、あ、そうか。」
「そう、その90度横向きにあるのが、虚数単位 i だ。
虚数平面上で、* i は、90度横を向くことに相当する。
“まわれ右”の半分だから、“右向け、右”。」
「ということは・・・2つ掛けて i になる数は、90度の半分の45度ってこと?」
「その通り。
図を見てごらん、“リンの虚虚数”は、ちょうど45度の位置にある。」
「なるほど、複素数の掛け算は、“まわれ右”ってことなんだ。。。
あれっ、どちらかっていうと“まわれ左”かな?」
「そう、右か左かは、図を描いた人が勝手に決めた向きに過ぎない。
しかし、回り方が2通りある、ということは重要だろう。
2通りあるというのは、虚数には +i と -i が存在するということに同じだ。」
「ふーん、だから、+i と -i を“入れ替えても全く気付かない”、
右と左みたいに、どっちがプラスでどっちがマイナスでも同じってことだね。」
「・・・マスター、なかなか数学の才能があるな。」
「でしょ、でしょ、って、あれ?!」
Gはしまった、って顔してた。へへー。
「いや、どんな才能も磨かなければ光らない。
ところで、“リンの虚虚数”には、もう1つの答がある。
どこだかわかるか?」
「えーっとぉー、ぐるっと回って90度になるところって、45度しかないと思うんだけど。。。」
「才能、取り消し。」
「えー、待って待って、いっしょうけんめい考えるよ、
・・・ぐるぐるぐるぐるっと回って・・・あっ、ここ!」
「正解。180+45=225度の点、数にすると (- 1/√2 - 1/√2i) だ。」
「ぐるっと回って一回転して、90度のところで止まるんだね。」
「そうだ。2回掛けて i になる、ということは、式にすれば x^2 = i 。
これは二次方程式だから、答は2つあるわけだ。」
「なるほどねー、なんか、テストの落とし穴みたい。」
「一見イジワルのように見えるが、答がいくつあるのかは、かなり大事なセンスだぞ。
もう1つ応用問題、3つ掛け算して -1 になる数は?」
「かんたん、かんたん、60度のところだよ。」
「答えの数は? センス、センス。」
「えっ、えーと、、、ひょっとして、答は3つあったりして・・・」
「顔色をうかがう前に気付いていたら、褒めるところだったがな。」
「えへへ、あと2つは、ぐるぐるぐるっと回って。。。あ、そうか、-1 だね。
もう1つは 300度、というか -60度のところ。」
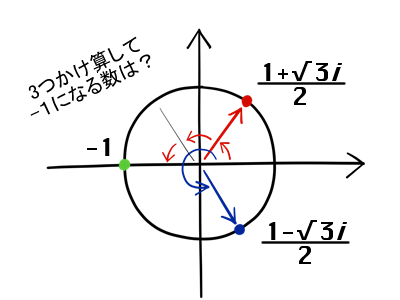
数にすると、-1, (1 + √3i)/2, (1 - √3i)/2 の3つだ。
これでもう、何回か掛け算して -1 になる数と、1 になる数のことがわかっただろう。
複素平面の円周上をN等分した点が、1のN乗根になっているわけだ。」
Gは、もう1つ新しい円を描いた。
「大事なところだから、もう1回言っておくぞ。
2回掛けて1になる数は、1 と -1 だ。
これは円周の上で、ちょうど0度と180度の2カ所にある。」
たしかに、円周を2等分している。
「次にわかりやすいのは、4回掛けて1になる数。
これは、0度、90度、180度、270度の4カ所だ。」
「えっと、、、数にすると、1, i, -1, -i の4つだね。」
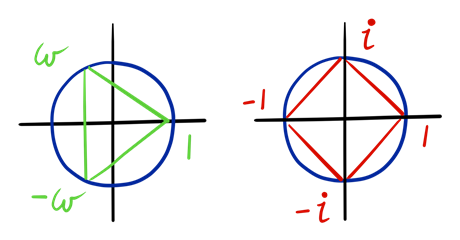
「そう、4つの数を線で結ぶと正方形になる。
ならば、3つ掛けて1になる数は、図の上で正三角形になるだろう。」
「0度、120度、240度・・・」
「そうだ、数にすると 1, (-1 + √3i)/2, (-1 - √3i)/2 の3つだ。
この1の三乗根 (-1 + √3i)/2 は、ωという記号で表すことがある。
いま、(-1 + √3i)/2 の方を ωとしてみたが、
実はもう一方の (-1 - √3i)/2 の方を ωとしても、結果は全く同じになる。
なぜかというと・・・」
「i と -i は全然区別がつかない、“対称性”があるから。」
おっと、Gはちょっと驚いたみたい。でも、もう才能って言わなかったよ。
「さて、それでは円周上に無い数の掛け算も見ておこう。
最初にやった掛け算、(1+i)・(-1-i) の矢印をみてごらん。
掛け算の答は、それぞれの数の角度を足したものになっているはずだ。」
「ほんとだ、45度+135度 = 180度 になってる。」
「さっきと違うのは、矢印の長さだ。
(1+i)という矢印の長さが√2、(-1-i)という矢印の長さも√2。
そして、答の矢印の長さは2となっている。
ということは?」
「矢印の長さは、長さ同士で掛け算すればいいんだね。」
「その通り。半径1の円周上であれば、長さは全部1だから、角度だけを問題にすればよかった。
それ以外の複素数には、角度と長さがある。
まとめると、複素数同士の掛け算は、
・角度は足し算
・長さは掛け算
といったことをすればいいわけだ。」・長さは掛け算
「でも、どうして掛けると回るんだろう?」
「そうだな、、、複素数が回転を表す行列と同型になっている、というのが解りやすいかな。」
「回転を表す行列、ですかぁ〜。」
「その言い方だと、頭に入っていないようだな。
マスター、2次元平面上での回転行列は?」
「え、えーっと、サインとか、コサインとか、、、でも、そんなの覚えらんないよ。」
「覚えるのではなて、その場で考える。
線型変換ってやつは、2つの軸がどこに移るかだけを見れば全体がわかる。
2つの軸というのは、x軸の(1,0)と、y軸の(0,1)のことだ。」
そう言って、Gはまた丸の絵を描いた。
ほえー、きびしいなあ、、、
「うーんと、えーっと、これがコサイン、かな?」
「慣れていないのだったら、覚えるしかないな。
SとCの、字の形で覚えるんだ。」

「ここがSの形、ここがCの形になっている。ということは?」
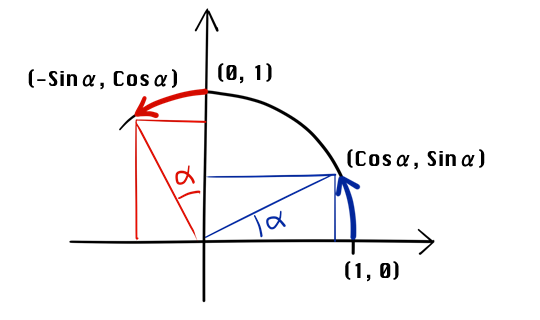
「ええと、点(1,0)を回転させると点(Cos(α), Sin(α)) 。
点(0,1)は、、、点(-Sin(α), Cos(α)) 。」
「その2つの点、4つの数字を並べたものが回転行列だ。」
xについて、(縦ベクトルで書いてある)
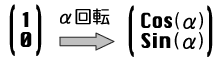
yについて、(縦ベクトルで書いてある)

両方合わせて左右に並べると、
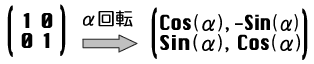
「記号がたくさん出てくると見にくいだろうが、いま大事なところは回転行列が
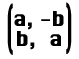
というパターンになっていることだ。
まず、これを覚えておこう。」
なるほど、全部丸暗記する必要はなくって、(1,0)と(0,1)の行き先を追えばいいんだ。
「次に、2回の回転を合わせることを考えてみる。
まずα度回転して、その次にβ度回転する操作を、連続で一気に行ったらどうなるか?」
「・・・えと、えーと、αとβを、足したらいいんじゃないかな、なんちゃって・・・」
「残念、足す、ではなくて、掛ける、だ。
回転の操作を表す行列を、2つ掛け合わせると、合わせて回転したことになる。
α度回転させる行列がA、β度回転させる行列がBだとしたら、
(α+β)度回転させる行列は、A*B になる。」
「なんで掛け算なの?」
「実はこれは話が逆で、ちょうど掛け算が変換の操作に一致するように、行列の掛け算の約束を決めた、というのが本音だ。
混乱の原因は、変換操作のことを“掛け算”という同じ言葉で呼んでしまったところにあると思う。
いっそ、数字の掛け算と、行列の掛け算は別物だと考えた方がいい。
最初に聞かされたとき、行列の掛け算のルールは、妙に複雑だとは思わなかったか?」
「思った、思った、きっとテストを難しくするために作ったんだろうって、思ったよ。」
「じゃあ、その難しいやつを、やってみるか?」
・・・あたしは絶望的な顔をして見せた。
「今回はやってみせよう、次回までに覚えてくること。」
「えー、宿題があるのー?」
「努力あるのみ。
回転の掛け算を、単純化したパターンで書いてみるぞ。」
α度回転行列
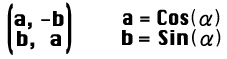
β度回転行列
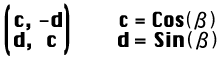
(α+β)度回転行列
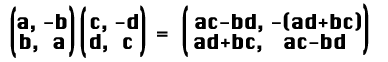
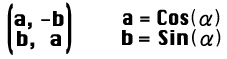
β度回転行列
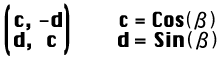
(α+β)度回転行列
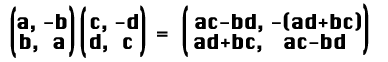
「ふーん、なんか結果は ac-bd と、ad+bc の2種類になるんだね。」
「それが大事なところだ。
この結果を見れば、Sin(α+β) と、Cos(α+β) がどうなるかが解るわけだ。」
「あ、それって、覚えるのがすごーく苦痛な公式!」
「そう、三角関数の加法定理だ。
行列の掛け算さえ覚えておけば、少しだけ記憶容量が稼げるぞ。」
そっかー、公式覚えられる人って、こうやって記憶容量稼いでたんだ。
「複素数の掛け算の話に戻ろう。
(a + bi)・(c + di) という掛け算の規則はどうなっているかというと、」
(a + bi)・(c + di) = (ac-bd) + (ad+bc) i
「あ、これって、さっきの行列の中身と同じだ。」
「その通り。回転を表す行列の中身と、複素数の掛け算の規則が同じものになっている。
これが、“掛けると回る複素数”の秘密だ。」
うーん、半分くらい、わかったような・・・
「学校では最初に、虚数とは“2乗して1になる数”なのだと教わる。
でも、それだとなかなかイメージが湧かない。
そこで、一度最初の虚数のことは忘れて、もっと別の角度から見てみよう。
2つの数字の組 a, b があって、それが平面上の回転 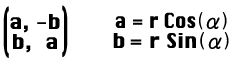
を表していたとき、この数字の組のことを複素数と呼んでいるのだ。」
「じゃ、複素数っていうのは、もともと“回転を表す数”のことだったの?」
「そういうことになるな。
“2乗して1になる数”と、“回転を表す数”は、実は同じ1つのものだった、というわけだ。」
「あれ、・・・よーく見ると、いつの間にか "r" って文字が増えてるんですけどー。」
「気付いたか。
話が回転だけだったら、円の上にある数だけにしか当てはまらない。
それを平面全体にあてはめるには、角度だけでなく、“矢印の長さ”も変える必要がある。
上で r と書いたのは、矢印の長さの拡縮率のことだ。」
こっそり黙って入れたのかしら、、、Gってそのあたりがイジワルなんだよねー。じぃー、、、
「な、なんだその目は。」
「べっつにー。」
「そんなに疑うなら、r を入れてやり直しても、同じパターンが出てくるぞ。。。
ああ、それ、宿題にちょうどいい。」
「えー! もういいよー、ね、ね、もうわかったからさ。」
「まだまだ。
複素数と回転、複素数と三角関数には、深い結びつきがある。
今日はそこまで行けないが、いずれ出会うときが来るだろう。」
ほへー、複素数って、まだまだ奥が深いんだー。
|
※ 回転行列についての補足.
Sin, Cos の図から回転行列を導き出す手順は、かなりややこしいものです。
何が縦ベクトルで、何を横ベクトルとするのか?
プロットした点が回転するのか、それとも地の紙面の方が回転するのか?
よく分からなくなったら、以下の式をもとにじっくり考えてみてください。
Sin, Cos の図から回転行列を導き出す手順は、かなりややこしいものです。
何が縦ベクトルで、何を横ベクトルとするのか?
プロットした点が回転するのか、それとも地の紙面の方が回転するのか?
よく分からなくなったら、以下の式をもとにじっくり考えてみてください。

