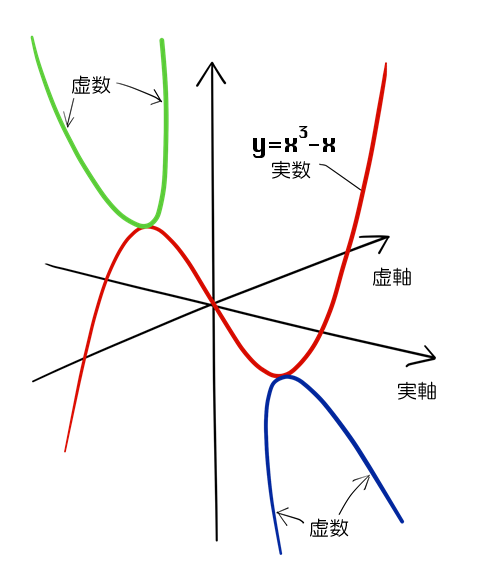
三次関数、隠されたグラフ
2009/09/15
 |
 |
数学夜話・第4回:三次方程式 に、三次関数を複素数の範囲で描いたグラフが出てきました。
y = x^3 - x ・・・(1)
という関数は x:複素数 → y:実数 の範囲で、どのような形になるのか?x = u + v i として、u, v, y の3次元空間にグラフを描き出してみましょう。
以下の説明は、
『隠されたグラフ(3次関数の分類)』(島根県立益田高等学校)
というレポートに記載されていたものです。
というレポートに記載されていたものです。
まず、(1)式の x を u + v i と置きます。
y = (u + v i)^3 - (u + v i)
= u^3 - 3 u v^2 - u + (3 u^2 v - v^3 - v) i
= u (u^2 - 3 v^2 - 1) + v (3 u^2 - v^2 - 1) i ・・・(2)
ここでは y を実数に限定したグラフを描こうとしているから、= u^3 - 3 u v^2 - u + (3 u^2 v - v^3 - v) i
= u (u^2 - 3 v^2 - 1) + v (3 u^2 - v^2 - 1) i ・・・(2)
(2)式の虚数部分、
v (3 u^2 - v^2 - 1) = 0
になっています。ということは、
v = 0 ・・・(a)
または
3 u^2 - v^2 - 1 = 0 ・・・(b)
のいずれかである、ということです。(a) が成り立つ場合:
v = 0 のとき、(2)式は
y = u (u^2 - 1)
= u^3 - u
となります。= u^3 - u
これって要するに、最初の(1)式 y = x^3 - x の実数部分ということですね。
このグラフを u:y平面で見たら、こうなっています。
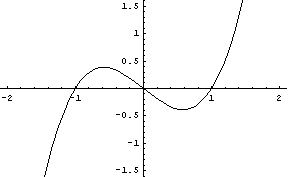
(b) が成り立つ場合:
(b) の式を見ると、
3 u^2 - 1 = v^2
u^2 - 1/3 = 1/3 v^2
ですから、u が実数となるのはu^2 - 1/3 = 1/3 v^2
u <= -√1/3 または √1/3 <= u
の範囲です。つまりこれは、0の近辺を除いた上と下の2カ所に、虚数部分のグラフが分かれて出てくるということです。
(b)式を v について解けば
v = ±√(3 u^2 - 1)
これを用いて (2)式から v を消去すれば、グラフを u:y平面に投影した形がわかります。
y = u (u^2 - 3 (3 u^2 - 1) - 1 )
= - 8 u^3 + 2 u
= - 8 u^3 + 2 u
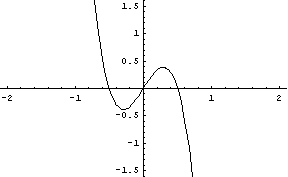
一方、(b)式を u について解けば
u = ±√(v^2/3 + 1/3)
これを用いて (2)式から u を消去すれば、グラフを v:y平面に投影した形がわかります。
y = ±√(v^2/3 + 1/3)・( -(8/3)v^2 - 2/3 )
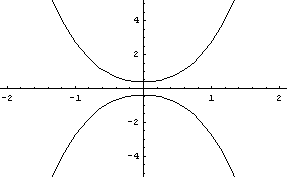
以上の平面に投影されたグラフを組み合わせると、
u:v:y3次元空間上でのグラフ形状が浮かび上がってくるでしょう。