「さて、前回の続きで、今回は四次方程式の解法を調べてみよう。」
「・・・なんかもう、ストーリーパートを完全に無視しちゃってるね。」
「いろいろ試してみたのだが、やはりストーリーと方程式を両立させるのは無理があると判断したのだ。」
「やっぱり方程式って、おもしろいお話にはならないんだねー。」
「分かってくれば、方程式だけで充分おもしろいと思うぞ。」
「あたしはストーリーだけでもいいんだけどなぁ。」
「こっちがメイン、ストーリーはオマケだ。」
「あたしの活躍がメインじゃなかったのか。」
「マスターみたいなのがいるから、少しでも親しみやすく、いろいろ工夫しているんじゃないか。」
「へいへい。じゃ、本日のメイン、いってみよっか。」

「四次方程式の解法も、三次方程式と同じように、リゾルベントと補助方程式を作ることになる。
　最初にリゾルベントだが、どんな式を作ればいいのかな？」
「ええと、答を入れ替えても、値が変わらないような式を作ればいいんだよね。
　四次方程式の答は４つだから、４つの数の入れ替え方は 4! = 4・3・2・1 = 24通り。
　それを１つ下の三次方程式にしたいのだから、３通りの値にまとまるような式を作ればいいんだ。」
「その通り、よくわかっているじゃないか。」
「で、ヒントは？」
「少しは自分で考えたのか？」
「そんなの時間のムダだよ、だって難しいんだもん。」
「はぁ・・・」
Ｇは、ため息を漏らした。
「まずは三次方程式の真似をしてみたらどうだ。」
「了解、じゃ、さっそく真似してみると、、、
　三次方程式だと複素平面上を１２０度ずつ、３分割で１回転してたよね。
　だったら四次方程式は９０度ずつ、４分割で１回転すればいいのかな。」
「その考え方で行くと、ωに相当するものは何だ？」
「９０度のところだから、、、虚数単位ｉだよね。
　そっか、そんな感じで真似したらリゾルベントは
　　(x1 + i x2 + i^2 x3 + i^3 x4)^4
　= (x1 + i x2 - x3 - i x4)^4
　だね。」
「うむ、悪くはないが、それだと４回の操作で１回転するだろう。
　ということは、全24通り / ４回 = ６通り。
　x1〜x4 の入れ替えに対して、式の値は６通りに変化する。
　それだと補助方程式は６次方程式になってしまう。」
「うーん、うまくいかないなー。」
「実は四次方程式には、三次方程式に無かった事情がある。
　３は素数だが、４は２ｘ２という合成数だ。
　なので、４の場合には３の真似をするのに加えて、もう１工夫要る。」
「そんなこと言っても、もう工夫の余地ないんですけどー。」
「あきらめるな。
　１つの式でダメなら、もう１つ似たような式を作ってみたらどうだ。
　例えば回転を逆向きにして
　　(x1 + (-i) x2 + (-i)^2 x3 + (-i)^3 x4)^4
　= (x1 - i x2 - x3 + i x4)^4
　という式を作ってみる。」
「でも、これだってさっきと同じだよね。
　４回の操作で１回転するから、この式もさっきと同じように６通りになるよ。」
「２つの式を合わせてみたらどうだ。」
「へっ？！」
「２つの式を見て気付くことは、どちらも
　x1 -> x2 -> x3 -> x4 -> という入れ替えに対して、値を変化させないことだ。
　この入れ替えが４通りある。」

「それで？」
「そして、最初に作った式と、次に作った式を比べると、
　x2 と x4 を入れ替えたものだということに気付く。」
「そうだね、回転のイメージだと、９０度と２７０度のところを上下逆さにしたみたいだね。」
「ということは、最初の式と、次の式の値を互いに入れ替える方法は４通りある。
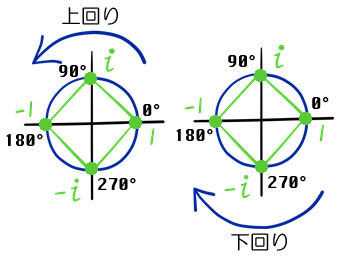
　これ、わかるか？」
「えーと、上下逆さにして、そこから９０度ずつ回したのが４通り。」
「そういうことだ。」
「そこでだ。２つの式を合わせて
　　(最初の式) + (次の式)
　という式を作ってみたら、この合わせた式の値を変えない入れ替えは、何通りある？」
「むむー、まず１つ１つの式の値を変えないのが４通りでしょ。
　そんでもって、前後の式の値が入れ替わるのが４通り。
　合わせて８通りの入れ替えについて、値を変えないみたい。」
「４つの x1〜x4 の入れ替え方法が２４通り。
　その中の８通りの入れ替えについて、この合わせた式は値を変えない。
　で、24 ÷ 8 は？」
「３。。。あ、できた。」
「できたね。
　この３つの式は、24通りの入れ替えを、３通りの値にまとめるリゾルベントになっている。」
「あとはその３つの値を使って三次方程式作って、って、うわー、涙が出るくらいたいへんそう。」
「確かに、まともに挑んだら、かなり複雑な計算になるな。」
「・・・この辺で、やめとこっか。」
「マスターはすぐ怖じ気づくのだな。」
「あたしは無謀なことはしない主義なの。」
「ぐうたら主義だな。しかし、今の場合は正しい判断だ。
　たとえこの三次方程式が解けたとしても、その先、最終的な４つの答にたどり着く段になって困ってしまう。」
「そうそう、これだけ複雑な式だと、その先もたいへんだよ。」
「４乗が２つも入っている連立方程式だから始末が悪い。
　ここまで複雑にならなくても、もっと良いリゾルベントが他にもある。」
「え、どんなの、どんなの？」
「初心に帰って、ヤマカンで探してみたらどうだ？」
「いじわるぅ。」
「自分の頭で考えることが大事なんだ。」
「くうぅ。じゃ、初心に帰って、まず
　　x1 + x2 + x3 + x4
　って式は、、、だめだね。どんなに x を入れ替えても、結果は１通り。」
「・・・」（無言）
「じゃ、じゃあ、ちょっとだけ変えてみよっかなー、、、てきとーに引き算にして、
　　x1 + x2 - x3 + x4
　だと、だめみたいなよーな、、、」
「・・・」（無言）
「それじゃ、半分だけ引き算にして、
　　x1 + x2 - x3 - x4
　とか・・・」
「それ、正解。」
「えっ、なんかやけに簡単に見つかったね。」
「難しく考えずに、とにかくやってみるっていうのも、以外に効果がある。
　確かめてみよう。その式を
　　(x1 + x2) - (x3 + x4)
　という風に見る。
　この式の値を変えない入れ替えは、次の４つだ。」
「でも、目指すのは８通りだから、あとの４通りはどうしようか。」
「入れ替えたら値が変わらないのではなくて、入れ替えたら値がマイナスになる、というものがあるだろう。
　前半の (x1 + x2) と、後半の (x3 + x4) をガサッと大きく入れ替える。」
「えっと、つまり x1 ←→ x3 と x2 ←→ x4 を同時に行うってことだね。
　あと、x1 ←→ x4 と x2 ←→ x3 っていう組み合わせもあるね。」
「そうだな。
　式の値を変えない入れ替えが４通り、式の値をマイナスに変える入れ替えが２通り。
　ということは、この式の絶対値を変えない組み合わせは全部で４・２ = ８通りになる。」
「値を変えない入れ替えの後に、マイナスに変える入れ替えを、続けてやった場合の数だね。」
「さて、絶対値が同じで、プラスマイナスだけが違っている数を、同じ値にそろえるには、どうしたらいいかな。」
「２乗してみるとか。」
「これで、できたろう。
　という３つの式は、24通りの入れ替えを、３通りの値にまとめるリゾルベントだ。」
「わ、できちゃった。」
「今度のリゾルベントの方が、さっきのものよりだいぶ簡単だ。
　実は、まだ別のリゾルベントが考えられる。」
「え、まだあるの。」
「 (x1 + x2) - (x3 + x4) という式を見てごらん。
　これとそっくりな式を、他にも作れないか。」
「えーっとね、真ん中の - を ÷ に変えてみるとか。」
「それは良いアイデアだが、(x3 + x4) = 0 だったときに困るだろう。」
「そっか。じゃ、+ のところを、掛け算に変える。」
　　( x1・x2 - x3・x4 )^2
「うむ、理屈上はこれでもいいのだが、さらに簡素化できて、実はこんな式でもＯＫだ。
　　x1・x2 + x3・x4
　調べてみてごらん。」
「ええと、
　４通りの入れ替えと、２通りの入れ替えの組み合わせで、４・２ = ８通り。
　確かにね。
　でも、こんな式、答を教えてもらったからわかったけど、自分で見つけるのなんて、ほとんど無理。」
「そうだな。理屈はそれなりに後付けできるが、最初に見つけたのは、試行錯誤の末だろう。」
「きっと最初はヤマカンで、いろいろやってみたんだね。」
「ああ、ヤマカンは言い過ぎかもしれないが、頭と手を動かしていろいろやってみたのに違いない。
　今見たように、リゾルベントは決して１通りではない。
　いろんなリゾルベントを考えることができて、それに合わせていろんな方程式の解法ができる。
　しかし、どんなリゾルベントであっても、“24通りの入れ替えをを３通りにまとめる”という基本は変わらない。」
「なるほどー。答の入れ替えとか、対称性とか言ってた意味が、ちょっとだけわかってきたよ。」

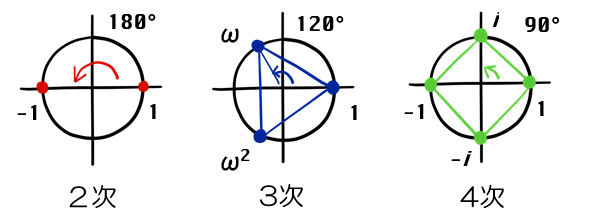
「整理してみよう。
　最初に３次方程式を真似て作った式、この形の式は“ラグランジュのリゾルベント”と呼ばれている。
　複素平面上の単位円を、角度でＮ個に分割したようなイメージだ。」
「これだと、二次方程式は
　ってことになるのかな。」
「そういうことになるな。
　リゾルベントという考え方で、二次方程式の解の公式を導くのは、こんな感じだ。」
「へー、ちょっと計算たいへんだけど、とにかく“ラグランジュのリゾルベント”で三次方程式までは機械的に解けちゃうんだ。」
「ラグランジュという人は、いわば“機械化の魔術師”だと思うな。
　彼は方程式の研究だけでなく、解析力学の創始者でもある。
　“数学に基づく思考経済”という点で、ラグランジュのアイデアには、一本筋の通ったものが感じられる。」
「でも、数式だらけで、なんかとっつきにくい感じ。」
「マスターのような数式アレルギーにはキビシイかもな。
　方程式の歴史も、幾何学的なイメージから、抽象的な記号へと、時間をかけて進化してきた。
　それと同じで、マスターも時間をかけて、少しずつ記号化していけばいい。」
「うー、先が長いんだー。」
「さて、残る２つのリゾルベントについてだが、
　　( (x1 + x2) - (x3 + x4) )^2
　このリゾルベントを元にした、四次方程式の解法がある。
　実質的に、オイラーの解法と呼ばれているものと同じなのだが、今回は省略しよう。」
「ふうっ。」
「最後に
　　x1・x2 + x3・x4
　というリゾルベント。
　これが以前やってみた、フェラーリの解法に対応している。
　なので、このリゾルベントを用いて最後まで方程式を解いてみよう。」
「えと、リゾルベントから補助方程式を作ってみるんだよね。」
「うぇー、また涙のこぼれるような計算だよー。」
「仕方ない。ここはバトンタッチしよう。」
「この補助方程式を、以前のフェラーリの解法の、途中で出てきた三次方程式と比べてみてごらん。
　実質的に同じものになっているはずだ。」
私は以前のノートを見直してみた。（第５話参照）
「ぱっと見には違う式みたいに見えるけど。」
「以前解いたときと、記号が少しずつ食い違っているな。
　以前のときは、もとの方程式を簡単にして x^3 の項を消去した
　　x^4 + a x^2 + b x + c = 0
　からスタートしていた。
　なので、今回の結果と合わせるなら
　・今回の結果の x^3 の係数、a=0 にする。
　・今回の結果に合わせて、前回の結果を１文字ずつずらす、a -> b、b -> c、c -> d 。
　・t = 2y となっている。
この３つの補正を行ってみよう。」
「ほんとだ、同じになってる。」
「つまり今やってきた計算は、フェラーリの解法をリゾルベントという視点から見直したものだ。」
「なるほどね。でも、前にやったことを、ますます難しくしているだけみたい。」
「ただ答を出す、という目的のためだけなら、そうだろう。
　しかし今やっていることは、“なぜ五次方程式は解けないか”その秘密を探るため、
　方程式の解き方を見直していたところだ。
　こうして見直してみると、リゾルベントという式が、重要な働きをしていることに気付くだろう。」
「そうだね。
　結局わかったのは、２４通りを３通りに減らすプロセスが入ってたってことだね。」
「これで核心部はクリアーした。
　あとはひたすら計算を推し進めるだけだ。」
「・・・やっと解けた。こうして見ると、けっこうたいへんだね。」
「いかんせん四次方程式だからな。
　二次方程式と比べれば、複雑さは段違いだ。
　四次方程式の解の公式を、無理矢理一本にまとめようとすれば、こうなる。」



「ぎょえー！ もういいよ、おなかいっぱい。」
「ついでに、三次方程式はこんな感じだ。」



「ふぇーん、こんなの絶対覚えらんないよー。」
「別に覚える必要は無い。
　必要であれば、説明でやったように１ステップずつ進んでゆけば良いし、
　答が知りたいのなら、コンピューターが充分な精度で出してくれる。」
「じゃあ、公式の意味って、あんまり無いのかなあ。」
「そうだな。公式自体よりも、途中のステップの方が大事だな。
　結果を覚えるよりも、公式を作り出すための考え方を知っておいた方が、ずっと応用が効くぞ。」