凛「・・・Ｇってさ、暗ーい過去があったんだね・・・」
Ｇ「・・・気にするな、もう昔の話だ。」
凛「なんだか、Ｇがかっこよく見えてきたよ。」
Ｇ「だったらいままでは、どう見えていたんだ。」
Ｇがまた、ため息を漏らした。
咲「・・・えっ、ひっく、ひっく、、、」
凛「咲ちゃん、泣かないの！」
咲「・・・だって、ＧさんもＡさんも、かわいそうですぅ。。。」
Ａ「そんなに悲しむことはない。
　Ｇも、私も、こうしてその後の数学の発展を見守ってきたんだ。
　時間はかかっても、人類は着実に進歩しているんだよ。」
咲「・・・うん。」
Ｇ「思えばもう２００年近くも経とうとしているのに、
　方程式に潜む形は、今なお難解な理論だと言われている。
　２００年前に、理解が得られなかったのは、当然かもしれないな。」
凛「時代を進みすぎていたんだね。」
咲「・・・大丈夫だよ、きっと私たちが追いついてみせるから。」
Ａ「それは頼もしいな。ならば、私たちも安心だ。」
Ｇ「ならば、２００年前には誰も理解し得なかった、方程式の形を見てみることにしようか。
　前回挙げた、体についていま１つの重要概念は、こんなものだった。」
　２： 代数体の形というのは、空間の鏡像反転、回転する三角形などの“入れ替えパターン”ってこと。
Ｇ「この“入れ替えパターン”のことを、現在では“群”と呼んでいる。」
凛「“群”って、グループのこと？」
Ｇ「正確な定義は後にして、まずは実際に x^3 - 2 = 0 という方程式の形を見てみよう。
　この方程式の答は、³√2, ³√2ω, ³√2ω^2 の３つ。
　最小分解体は Ｑ(³√2, ω) だった。」
凛「そんでもって、その体の同型が、三角形みたいにグルグル回転してたんだよね。」
咲「それに合わせて方程式の答も入れ替わってますよね。
　　α → α ω → α ω^2 （α=³√2）の系列と、
　　ω → ω~ （√3ｉを -√3ｉ に置き換える）系列
　この組み合わせの６パターン。」
Ｇ「この６パターンの入れ替えは、三次方程式の形そのものなんだ。
　以前、三次方程式の解法を詳しく調べたことがあったが、思い出してごらん。
　何か思い当たることはないか？」（数学夜話 第６回）
凛「ああ、リゾルベント、答の入れ替えってやつ！」
咲「リゾルベントって？」
凛「確か三次方程式って、３つの答の入れ替えが６通りあったじゃない。
　それを２通りにまとめられれば、二次方程式になって、解くことができるって。」
咲「あっ、それって三次方程式の解法のことですね。
　そういえば、この６パターンっていうのは、３つの答の入れ替えそのものですね。
　あと、その６パターンが２系列に、３・２になっているっていうのも、解法そのものになっている。」
凛「そっか、３・２になっているから、２通りにまとめることができるのか・・・」
咲「そうですよね、その２パターンっていうのは、二次方程式の２通りと、同じですよね。」
凛「わっ、わっ、これって、ひょっとしてすごいことだよ。
　咲ちゃん、私たち、大発見しちゃったよ！
　方程式の解法 = 方程式の答の入れ替えパターン = 代数体の入れ替えパターン！」
Ｇ「それを２００年前に思い付いていれば、間違いなく大発見だ。」
Ａ「でも、こうして今追いついたのだから、再発見ってことでいいんじゃないかな。」
凛「再発見ね、フーン、再発見！」
咲「・・・ＧさんとＡさんが、教えてくれたんじゃ・・・」
Ｇ「方程式の解法 = 方程式の答の入れ替えパターン = 代数体の入れ替えパターン。
　ここには何か、全体を貫く、隠された形のような概念がある。それが“群”だ。」
凛「隠された形、それって、なんとなくイメージできるよ。
　ほら、三角形がグルグル回転しているみたいってことでしょ。」
Ｇ「そのイメージは当を得ているぞ。
　三次方程式の群は、１枚の正三角形の板が持つ対称性の群と、同型になっている。
　しばらくは方程式を離れて、正三角形の板の操作を考えてみることにしよう。」

凛「正三角形の板の操作って、１２０度回転ってこと？」
Ｇ「正三角形の板を動かして、もとの正三角形にぴったり重ねる操作には、
　どれだけの種類があるかという問題だ。」
咲「あ、だとすると、１２０度回転だけじゃないですね。
　こうやって、パタンって裏表ひっくり返して、２つの頂点を入れ替えてもぴったり重なりますよね。」
Ｇ「その通りだ。
　正三角形の操作には、１２０度回転、２４０度回転、
　裏表をひっくり返す方法には３つの軸があるから３通り、これだけある。
　通常はこれに“全く動かさない”操作を含めて、６通りの操作があるとしている。」

凛「たしかにこれって、体の同型写像と全く同じだね。
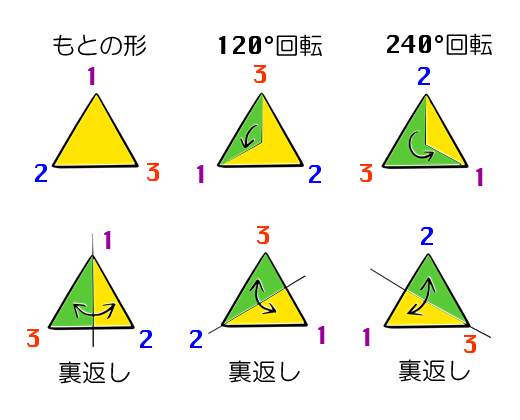
　三角形の回転が、α → α ω → α ω^2 ってことで、
　三角形を裏返すのが、ω → ω~ ってことだ。」
咲「方程式の３つの答の入れ替えの方は・・・」
Ａ「３つの答を 1, 2, 3 として、全部の入れ替えパターンを書きだしてみようか。
　表記法のお約束だけど、入れ替えを表すには、
　上に入れ替え前の数字を、下に入れ替え後の数字を並べて書く、といったことをする。」
Ａ「正三角形の３つの頂点に、1, 2, 3 という番号を付けて、
　移動後の正三角形の番号を調べてみてごらん。
　上の３つの要素の入れ替えパターンと、全く同じになっているよ。」
咲「ええと、回る、裏返す、、、ほんとだ。」
Ａ「３つの要素の入れ替えと、正三角形の板の置き換えは、同じ構造を持っていたということだね。
　ただ、いつでもそうなるとは限らない。
　４要素の入れ替えと、正方形の置き換えは異なっているよ。」
Ｇ「群というのは、こういった入れ替え操作の集合のことだ。
　正三角形のような多角形の板の操作には、“二面体群”という名前が付いている。
　要素の置き換えは“対称群”という名前だ。
　群に関する用語はたくさんあって、いっぺんに覚えるのは大変だ。
　さしあたって、方程式に重要なのは“対称群”。
　置き換え Symmetric の頭文字をとって、Ｓ₃（３は要素が３つという意味）という記号で表している。」
　　　　※ 置換群という言い方をすることもあります。
凛「３つの置き換えパターン、ええと、Ｓ₃っていうのかな、
　これはいつでも回転と裏返しの 3・2 に分類できるんだね。」
Ｇ「次に重要な点はそこだ。
　対称群Ｓ₃の要素のうち、回転に相当する３つだけを取り出しても、それはそれで１つの群を為す。
　一方、裏返しに相当する部分だけを取り出しても、それはそれで１つの群となる。
　回転して入れ替える操作だけを集めたものは“巡回群”と呼ばれている。」
凛「あれれ、群だらけ。っていうか、群って一体何だ？」
Ａ「そろそろ群の定義を挙げた方がいいな。」
凛「うわー、法律の文章みたい。」
咲「でも、１つ１つ確かめてみれば、要素の入れ替えは確かに当てはまっているみたいですよ。」
凛「あれ、あれれー、おかしいよ。
　“１２０度回転 * 裏返し”は、“裏返し * １２０度回転”と違ってるよ。
　ああ、あたまこんがらかるなー。」
Ｇ「それは結合法則ではなくて、交換法則だ。
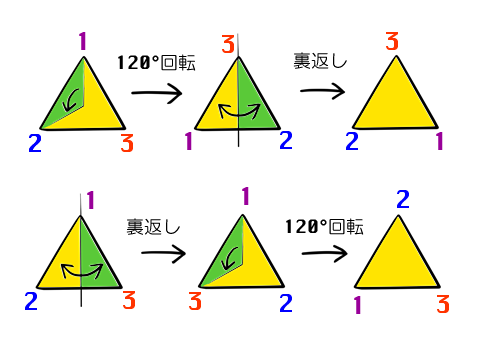
　群では、必ずしも a * b = b * a となっていなくても構わない。」
Ａ「交換法則 a * b = b * a が成り立つのは、群の中でも特別な場合だけだね。
　そういう特別な群には“可換群”という名前が付いているよ。」
凛「わっ、また新しい名前が出てきた。」
Ｇ「出てきたついでに、もう少し名前を覚えてもらおう。
　対称群Ｓ₃は、回転と裏返しの 3・2 に分けられる、という話をしていたところだった。
　回転に相当する３要素だけを取り出した集合は“巡回群”、
　この例のように、大きな群の中に含まれている、より小さな群のことを“部分群”と言う。」
凛「ふわー、まず“巡回群”からふわふわだよ。」
咲「回転だけってことですよね。
　だったら、ひっくり返しのない、車輪みたいに真ん中が止めてある三角形だと思えばいいんじゃないかな。」
Ｇ「そう、同じ３つの要素でも、動きに制限が加わっているものと思えばいい。
　先の入れ替えパターンの表記法を使えば、こんな風になる。」
凛「なるほど、同じ相手でも、動き方が違えば、違う群ってことなんだ。」
咲「この表記って、いつでも上の列は 1,2,3 ですね。
　慣れちゃえば、上の列が無くてもわかりますね。」
Ａ「実は、巡回置換の表記には、省略形があるんだ。
　　1,2,3
　　2,3,1
　のことを、ただ (1, 2, 3) と一列に書く。
　この省略形の読み方は、1→2, 2→3, 3→1 という意味だ。
　１つずつスライドさせるように読む。
　単に下の列だけを取り出したものとは違っているから、注意が要るぞ。」
咲「じゃあ、省略形で巡回群を書き直すと、こんな風になるのかな。」
Ａ「そういうことだね。(なし) は、何も動かさない単位元ということだろうけど、
　カッコよくするなら、e とでも書いておけばいいと思うよ。」

Ｇ「こうやって実際に要素を書きだしてみれば、部分群の意味がよくわかるのではないかな。
　正三角形の対称群には６つの元があったが、その中の３つを取り出したものが、やはり巡回群という小さな群になっていた。
　この関係が、“部分群”だ。」
凛「一部分だけの群ってことだね。もう言葉には驚かないぞ。」
Ｇ「三角形の操作から想像が付くのだが、2・3 = 6 のように、群の元は組み合わせの掛け算で成り立っていることがある。
　もし部分群があるときは、その元の数は、必ずもともとの群の元の数の約数になっている。」
凛「えっと、３は６の約数だってことだね。」
Ｇ「そう、なので、元の数が６の群に部分群があるとすれば、
　その部分群の元の数は、２か３になるはずだということがわかる。
　あと、ある群の元の数のことを“位数”と言っている。
　いちいち元の数、元の数、といっていると大変なので、これも用語として覚えてもらうしかない。」
凛「また新出単語。」
咲「位数６の群の、部分群の位数は３か２となっている。」
Ｇ「部分群の位数は、もとの群の位数の約数となっている。
　これはラグランジュの定理と呼ばれている。」
咲「ラグランジュさんて、何でもやってるんですね。」

Ｇ「さて、部分群が 2・3 = 6 のような組み合わせの掛け算になっているということは、
　その反対に、群の割り算といったものが考えられる。」
凛「群の割り算、って、どういうこと？」
Ｇ「位数で言えば、6 ÷ 3 = 2 。
　この割り算の答となっている“２”についても、それに相当する群があるということだ。
　三角形で言えば、裏表をひっくり返すという操作が、位数２の群に相当する。」
凛「ひっくり返しって、{ (何もしない), (ひっくり返す) } っていうだけの群？」
Ｇ「ああ、位数が２だけの簡単な群だが、それでも立派な群であるには違いない。」
咲「ちっちゃい群って、なんかかわいいね。」
Ａ「咲にかかると、何でもかわいくなってしまうな。」
凛「あたしには、何でも群になっちゃうように見えるよ。
　ええっと、つまり・・・
　　（正三角形を操作する群）÷（回っている群）＝（ひっくりかえし群）
　ってことなのかな？」
Ｇ「ニュアンスとしてはそれでいいんだが・・・
　ひっくりかえし群だとカッコが付かないから、もう少しまともな呼び方をしよう。
　ある群Ｇを、部分群Ｈで割った割り算の答を“商群”と呼んでいる。」※※
凛「じゃ、かわいいひっくり返し群は、商群になっているんだね。もう何でも来いっ。」
咲「ええと、位数の割り算ならできるけど、“群の割り算”ってどういうことなのかしら。
　集合を、集合で割るってことですよね。。。」
Ａ「“群の割り算”というのは、より正確には“類別”という操作のことなんだ。」
咲「類別？」
Ｇ「群を、同じ性質を持った元同士でグループ分けする操作のことだ。
　割り算というのは、元を正せば、大きな集合の中に、小さな集合がいくつ入るかという計算だろう。
　例えば 6 ÷ 3 だったら、要素が６の大きな集合の中に、要素が３の小さな集合が、ちょうど２つ入る。
　群の言葉に直すと、位数６の群Ｇの中に、位数３の部分群Ｈがあったとき、
　Ｈと同じ大きさのグループがＨ自身を含めて全部で２個できる。
　この２個のグループのことを“剰余類”と言う。」
咲「その“剰余類”の集まりが“商群”になっているんですか？」
Ｇ「わざわざ“類”と“群”で言葉を変えたということは、
　“剰余類の集合＝商群”になる場合と、そうならない場合があるということだ。
　でも、まずおおざっぱに“剰余類の集合＝商群”としてみようか。
　そうならない場合のことは、後で改めて取り上げよう。」

凛「ふにゅー、、、いま、あたしの頭の中の集合から、完全にはみ出したー。」
Ａ「わからなかったら、とにかく実例で試してみようか。」
咲「と、とにかく対称群Ｓ₃は、縦３列、横２行の表みたいに、きれいに並べられるってことですよね。」
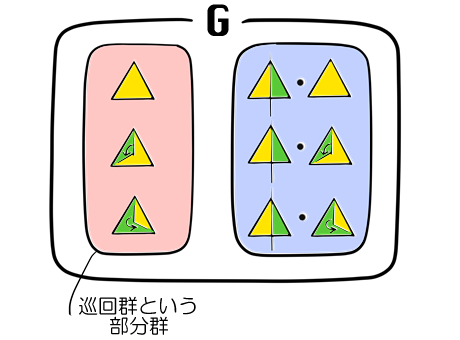
Ａ「ああ、その言い方だと、水平に並んでいる行が巡回群で、垂直に並んでいる個々の列が剰余類ということだね。」
凛「で、結局どこが“群の割り算”なのかなぁ？」
Ｇ「この表が２ｘ３＝６になっているのだから、６÷３＝２だろう。
　表の縦に相当する“剰余類の集合”が、即ち商群だ。」
凛「うぅー、表みたいに並ぶってので、わかったことにするよ。」

Ｇ「それでは、先ほど棚上げにした、“剰余類の集合＝商群”にはならない場合の話をするか。」
凛「もうパンクしそうだよー。ほんとにあと１っこだけだよ。」
咲「リンちゃん、大発見っていうのは、たいへんなんだよ。」
Ｇ「発見は、ひらめきだけでは完成しない。その後のフォローに大変な努力が必要なのだ。
　先ほどマスターは、必ずしも a * b = b * a になるとは限らない、ということを見つけただろう。」
凛「三角形のこと？
　“１２０度回転 * 裏返し”は、“裏返し * １２０度回転”と違ってたね。」
Ｇ「この問題が、群の類別でも生じる。
　先の説明では、元 a を部分群Ｈに掛け合わせるときに、a * Ｈ という順序で行っていた。
　しかし、掛け合わせの方法にはもう１つ、Ｈ * a というものもある。」
凛「えっ、それって違ってるの？」
Ｇ「三角形の例ではたまたま同じになるが、一般には違っている。
　a * Ｈ の類別を“左剰余類”、Ｈ * a の類別を“右剰余類”と呼ぶ。」
凛「うわー、またややこしいのが出てきた。右と左かぁ。」
咲「右と左が違うから、類と群は同じにならないのかな？」
Ｇ「もし“右剰余類”と“左剰余類”が異なっていたら、類別が２系統できてしまうことになる。
　こうなると、もとの群をピタリと１つに類別することができないので、商群というものができない。」
咲「でも、三角形はうまく類別＝商群になってましたよね。」
Ｇ「対称群Ｓ₃のように、右剰余類と左剰余類が一致してくれると、
　類別が１つに決まるので、うまいこと群にまとまってくれる。
　こんな風に、左右が一致する都合の良い性質を持った部分群を“正規部分群”と呼んでいる。」
凛「ああ、正規でよかった。」
咲「また新出単語・・・」
Ｇ「大事な新出単語なので、もう１度言っておくぞ。
　ある群Ｇを、正規部分群Ｈで割った答が、商群だ。
　商群は割り算の記号を真似て、G/H という書き方をする。
　Ｈが正規部分群でなければ、商群はできない。」
Ａ「方程式の形で取り上げるのは、この“正規部分群”だね。
　正規でない部分群は、方程式を解くための助けにはならないよ。」
咲「じゃあ、もう正規なものだけに着目すればいいですね。」
Ｇ「群については、まだまだたくさんの概念があるのだが・・・」
凛「ふにゅー、ふにゅー、、、」
Ｇ「マスターの要請により、ここまでで一区切りにしておこう。」
Ａ「とにかく専門用語がたくさん出てきたから、少しずつ慣れておこうね。
　数学の思考以前に、用語でまいってしまうぞ。」