今回から、数学夜話にＡと咲が加わった。
なんだか一気に賑やかになった。
いつも私がＧにいじられてばっかりだったから、思いっきり開放感！

Ｇ「今日は代数体について話そうと思う。」
凛「いきなり体かー。咲ちゃん、わかる？」
咲「ええと、聞いたことありますよ。
　確か、四則演算について閉じた数の集合、ってことだったと思う。」
凛「・・・すごい、咲ちゃん、天才。」
咲「そんな、、、これって、Ａに教わったことなんです。」
　咲ちゃんはちらっとＡの方を見た。
Ａ「咲は物わかりの良い子だったから、覚えも早かったね。」
　咲ちゃんは、ますます恥ずかしがった。

凛「Ｇの話って、最初は方程式から始まったんだよ。
　でも、気がついてみたら、なんだか方程式から遠く離れたところにきちゃったね。」
Ｇ「五次方程式は、単なる四次方程式の延長を越えた大問題だったということだ。」
Ａ「そうだね。五次方程式を解くという目的そのものよりも、解けないことを示すための過程の方が、
　後々ずっと大きな影響を与えていると思うな。」
Ａは、やっぱり数学の話になると、生き生きとする。
凛「結果よりも、過程が大事ってことだね。」
Ｇ「ちょっと違う気もするが・・・」
Ｇは、小さくため息を漏らした。
Ａ「いいじゃないか。
　とにかく五次方程式をきっかけにして、数体というものを考える契機ができたのだから。」
咲「体って、初めて聞いたときは、すごいことだと思いました。
　だって、無機質な数の中に、無限の階段があるなんて、思ってもみなかったもの。」
Ｇ「・・・そうだな、確かに、すごいことだ。
　そのすごいところで、まずは体と方程式の関係から探っていこうか。」
凛「前回は式の割り算ってところまで話したんだっけ。
　割り算って、なんとなーくわかるんだけど、数の範囲と割り算がどうなってんだか、ゴチャゴチャになっちゃった。」
咲「あのぅ、前回の話がわかるといいんだけど。。。」
Ｇ「そうだな、ちょっとおさらいするか。
　数の範囲と代数方程式は、深く関連している。
　かといって、必ずしも“ある１つの体 ←→ ある１つの方程式”が１対１に結びついているわけでもなかった。
　例えば、Ｑ(√２) という体では
　　x^2 - 2 = 0
　も
　　(x - 1) (2 x + 3) (x - √2) (x + √2) = 0
　も、解くことができる。
　他にも、この体で解ける方程式は無数にある。
　だとすると知りたくなるのは、どの体の中で、どんな方程式が解けるのか、ということだ。」
Ａ「Ｑ(√２)っていうのは、有理数Ｑに、√２という数を付け加えた代数体のことだよ。」
Ａが咲ちゃんに解説。咲ちゃん、解ってるから、すごいよ。
凛「それで式の割り算ってことになったんだっけ。」
咲「式の割り算って？」
Ｇ「方程式が解けるかどうかを見分ける方法の１つだ。
　例えば、ある方程式が (x^2 - 2) っていう式で割り切れれば、Ｑ(√２) の中で解けるってことがわかる。」
咲「ええと、因数分解っていうのと、同じことかな・・・」
Ａ「ああ、そうだね。
　因数分解っていうのは、正に式の割り算を押し進めたものだ。
　そこで問題になってくるのは √２という数と、(x^2 - 2) という式の関係だろう。」
咲「その (x^2 - 2) って式は、何なのかしら。」
凛「√２っていうのは、二乗したら２になる数ですよってことで、この式が出てきたんだよね。
　この式って√２の定義そのものってことで。」
Ｇ「しかし、考えてみると、ただ“√２成分”を含む式というのであれば、
　(x^2 - 2) にこだわる必要はないはずだ。
　別に(x^4 - 4) だって、(x^3 - 2 x) だって構わないだろう。」
凛「えー、そんなの、よけいなものくっつけてるだけじゃない。
　無駄のない (x^2 - 2) が一番ちっちゃくってかわいいんだよ。」
Ａ「かわいいかどうかはともかく、一番次数が低い式には違いないな。
　一番次数の低い、最も単純な式という意味はあるんじゃないかな。」
Ｇ「そう、なので (x^2 - 2) のことを √２の有理数上での“最小多項式”と呼んでいる。
　“最小多項式”とは、その数を解に持つ方程式の中で、最も次数の低い単純な式のことだ。」
咲「そうかー。 √２の拡大体で解ける方程式はいっぱいあるけど、
　その中で一番ちっちゃな方程式は１つしかないってことで、いいのかな？」
Ｇ「そう思ってもらって構わない。」
Ａ「厳密には定数倍だけ違う式というのもあるね。でも、細かいことは気にしなくていいだろう。」
Ｇ「とにかく最小の式を考えることで、
　　　“ある数αによる拡大体 ←→ ある１つの最小多項式”
　という１対１の結びつきができるわけだ。」
凛「最小以外の余計な式を無視しちゃえば、体と方程式は一心同体、ってわけね。あ、同体。」
話を聞いていると、ＧとＡって、テレパシーで通じてるんじゃないかって思う。
相手が何考えてるか、話さなくてもわかるみたいだ。
すごく仲良しなのかな（・・・怪しい妄想）。

Ｇ「もう１つ言葉を覚えておこう。
　いまは最小多項式という、式の方に着目したが、似たようなことが体の方についても言える。
　体を少しずつ拡大していって、ある方程式を初めて一次式に因数分解できるようになったとき、
　その体ののことを“最小分解体”という。」
凛「いちばん小さな体、うー、、、あたし因数分解って言葉、あんまり好きじゃない。。。」
Ａ「例えて言えば、整数で割りきれなかった割り算が、小数までいったら割り切れた、みたいな感じだね。
　理屈で悩むより、例を見て感触を掴んだ方がいいだろう。」

咲「あ、、、わかったよ。
　体を拡大してゆくと、いままで解けなかった式が、解けるようになる。」
凛「その、ちょうどギリギリ解けたところが最小分解体ってことだね。」
Ｇ「やはり習うより慣れろ、ってことだな。
　最小多項式も、ちょっと練習してみるか。
　例えば虚数単位ｉの最小多項式は？」
凛「二乗して−１になる数ってことだから、x^2 = -1 つまり x^2 + 1 = 0 ってことで、
　最小多項式は x^2 + 1 」
Ｇ「その通り。では、１の三乗根ωだったら？」
咲「ええと、(x^3 - 1) ってことかな。」
Ｇ「正解。次は難しいぞ、√２＋√３ の最小多項式は？」
咲「えっ、えっ、(x - (√2 + √3))^2 だったら、、、x^2 - 2(√2 + √3) + (√2 + √3)^2 で、だめだ、√が残っちゃうな。」
凛「(x - (√2 + √3))^4 でも、もっとだめ。。。あれー？」
Ａ「答は
　　{x + (√2+√3)} {x - (√2+√3)} {x + (√2-√3)} {x - (√2-√3)}
　= x^4 - 10 x^2 + 1
　だね。」
凛「あらら、きれいにまとまっちゃった。＋−が順番に出てくるんだ。」
咲「√2と √3の２つがあるから、四次式よりも簡単にはなりそうにもないね。」
Ｇ「本当はもっと簡単にならないかどうかチェックしなければならないところだが、いまはこれで良しとしよう。
　この方程式 x^4 - 10 x^2 + 1 = 0 は、Ｑ(√２, √３) という体の中で解くことができる。」
凛「あれっ、Ｑ(√２＋√３) じゃないの？」
Ａ「よく考えてみると、Ｑ(√２, √３) と、Ｑ(√２＋√３) は、数体としては全く同じものだね。」
咲「って、そうか、√２と √３ を組み合わせて √２＋√３ って式は作れるよね。
　・・・でも、反対に √２＋√３ って式から、√２と √３ を別々に出すことってできるのかな？」
Ｇ「 √２ + √３ = θ と置くと
　　√２ = (θ - (1/θ)) / 2
　　√３ = (θ + (1/θ)) / 2
　になっている。」
凛「うわー、パズルみたい。」
Ａ「これって偶然じゃないね。
　Ｑ(a, b) のように、２つの代数的な数によって拡大した体は、
　いつでも Ｑ(t) といった形で１つの数にまとめることができるんだ。」
凛「いつでもパズルになっちゃうのかな？」
Ａ「うーん、実際にまとめる方法はけっこう難しいので、例を並べてみるってことで勘弁して欲しいな。」
凛「なんとなく、パターンがあるね。」
Ｇ「実は、代数的な数はいつでも Ｑ(a, b) = Ｑ( a + C b ) という形にまとめられる。
　上の例では、たまたま C = 1 になっていた。
　２つの数 a, b が１つにまとまるのだから、同じことを繰り返せば、もっとたくさんの数を付け加えても
　 Ｑ( a, b, c, d, ・・・) = Ｑ(t)
　といった形で最終的に１つにまとめることができる。」
Ａ「Ｑ(t)みたいに、数を１個だけ付け足して体を拡大することを“単純拡大”って言うから、覚えておくといいよ。」

凛「うー、なんかわけわかんなくなっちゃった・・・」
Ｇ「どのあたりが？」
凛「だって、体の拡大って、 √２成分、√３成分、√５成分・・・って感じに、
　一個ずつ増えてゆくのかと思ったら、√２＋√３を合わせていっぺんにできるんでしょ。
　だったら、一個ずつ増えてくのは、あまり意味がないのかなー、なんて思ったりして。。。」
Ｇ「そこのところは、しっかりしたイメージを持つべきだな。
　おそらくリンは、体の拡大というものに、漠然と、だんだん大きくなる、
　といったイメージしか持っていないのだろう。」
凛「違うの？」
咲「あたしも、そんな感じだよ。」
Ａ「体の拡大は、ただ漠然と大きくなるのではなくて、一個ずつ次元が増えてゆく、といったイメージなんだ。」
凛「次元？ ２Ｄ、３Ｄ、っていう、次元のこと？」
Ａ「そう、二次元、三次元、の次元。
　しかも、体の拡大の場合は、３よりももっと大きな次元が登場することになるね。」
凛「３より大きな次元って、もうたくさんなんですけど。。。」
Ｇ「そう言うな。物理的な空間というよりも、空間の性質を数にあてはめてみたってところだ。
　リンは既に、複素平面というものを知っているだろう。」
凛「複素平面って、確かに二次元の空間だね。」
Ｇ「その二次元空間の持つ性質とは、何だかわかるか。」
凛「いきなり空間の性質ったって、、、直角に広がってるってことかな？」
Ａ「いい答だと思うな。その直角という性質が大事なんだ。
　確かに、複素平面では、実数軸と、虚数軸が直交している。」
Ｇ「ならば、直交している、という意味は、一体どういうことだろう。」
凛「だんだんイジワルクイズみたいになってきたなあ。。。９０度ってことかしら。」
Ｇ「感覚的には９０度なのだが、実際には、虚数がどこにあるのかわからないのだぞ。
　三角定規をもってきて、ほら、ここが９０度、と言って見せることができないだろう。」
凛「だからイジワルなんだよー。」
Ｇ「虚数はイジワルだから、三角定規を使わずに、数の性質だけで直交を示す必要に迫られる。」
咲「あのぅ、数の性質だけで言いえば、全然別の違ったもの、バラバラ、ってことじゃないかしら。」
凛「全く別の、違う種類のものだってこと？」
Ｇ「良い着眼点だ。
　種類もあるけど、もっと大事なのは、お互い同士の関係にある。
　直角の場合、一方を動かしても、他方に全く影響を与えない。
　ある数の虚数の値を変えても、実数の値は全く変わらない、という性質がある。」
凛「すごくあたりまえ、って気がするんですけど。」
Ａ「逆に、軸が直角ではなく、斜めに交わっているグラフを想像してみるといい。
　一方の値の変化が、他方の値にも影響を及ぼしている。
　つまり直角というのは、お互いが縛られることなしに自由に動ける、独立な関係ってことだよね。」
咲「自由恋愛みたいなものですね。」
咲ちゃんったら。。。
Ｇ「その例えはよくわからないが。。。
　とにかく、互いに無関係に、独立に動けるということが、直交を特徴付けているのだと言える。」
凛「あ、なんとなくわかった気がするよ。
　勝手に動いてもいいから、ｉを−ｉに入れ替えても、全く区別がつかないんだ。」
Ｇ「いい所に気がついた。
　複素平面というものが最初からどこかに存在していたと考えるより、
　互いに独立な２つの数は、平面として表すことができる、と思った方が納得がゆくだろう。
　互いに独立な３つの数は、立体として表すことができる。
　互いに独立な４つの数は、きっと四次元空間のようなもので表すことができる。」
咲「それが次元って言ってた意味なんですね。」
凛「数を並べているだけと思えば、そんなに怖くもないか。」

Ｇ「では次に、有理数に√２を付け加えた体 Ｑ(√２) を考えてみよう。
　複素平面と似たようなアイデアで、この数体を“√２有理数平面”みたいなもので表すことができないか。」
凛「えーと、横軸が有理数Ｑ、縦軸が√２ってこと？」
Ｇ「そう、縦軸は、正確には√２かける有理数。
　この平面上にある有理数点は、Ｑ(√２) を表している。」
咲「Ｑ(√２) も、二次元平面と考えればいいんですね。」
Ｇ「では、もう１つ増やして、√３を追加したら？」
凛「有理数の軸、√２の軸、√３の軸で、三次元の立体になるのかな。」
Ｇ「残念ながら、Ｑ(√２, √３) はもう１つ多い、四次元になっている。」
凛「えー、なんでー。どっからもう１次元湧いてきたの？」

Ａ「もう１つ、√２ｘ√３＝√６の軸、というものがあるんだ。
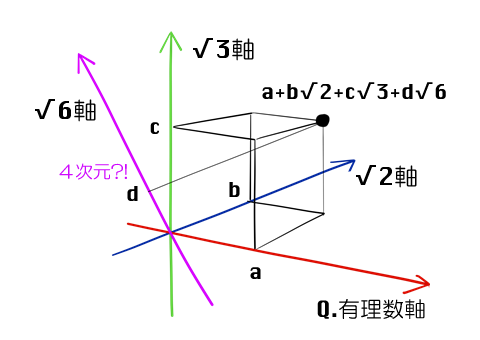
　直交の意味を考えてみよう。
　ある数が a + b √2 + c √3 と表いう形で表されていたとすると、√6 はどこに入るのかな？
　それが a + b √2 + c √3 + d √6 という形になっていれば、b の値を変えても、残りの a, c, d には影響を与えないよね。」
凛「うーん、“自由恋愛”だったら、√6 は別にしなきゃだめか。」
Ａ「√２と√３を付け加えた時点で、√２ｘ√３＝√６も自ずと体の中に入ってきてしまうんだ。
　よくわからなかったら、最小多項式に戻って考えてみるといい。
　Ｑ(√２, √３) の、最小多項式は何だろう。」
咲「さっき Ｑ(√２, √３) ＝ Ｑ( √２＋√３) って言ってたし、
　√２＋√３ の最小多項式は、確か
　　{x + (√2+√3)} {x - (√2+√3)} {x + (√2-√3)} {x - (√2-√3)}
　= x^4 - 10 x^2 + 1
　でしたよね。」
Ａ「そう、その最小多項式は四次式になっているだろう。
　だから、体の空間も四次元なんだ。」
凛「あれー、素直に (x^2 - 2)(x^2 - 3) でいいんじゃないの？
　これでも４次式だから、四次元になるよね。」
Ａ「いまはたまたま４次式になるように見えたけど、少し違うんだ。
　√をもう１つ付け加えて、Ｑ(√２, √３, √５) だったら、どうなると思う？」
凛「(x^2 - 2)(x^2 - 3)(x^2 - 5) で、６次式の六次元でしょ。」
Ａ「ところが√の掛け算の組み合わせを考えると、
　空間の軸は Ｉ, √２, √３, √５, √６, √10, √15, √30 の８つになる。
　ということは、体の空間は８次元だ。」
凛「うぅ・・・。」
Ａ「Ｑ(√２, √３, √５) の最小多項式は、
　　(x + (+√2 + √3 + √5))(x + (-√2 - √3 + √5))(x + (+√2 - √3 + √5))(x + (-√2 + √3 + √5))
　　　(x + (+√2 + √3 - √5))(x + (-√2 - √3 - √5))(x + (+√2 - √3 - √5))(x + (-√2 + √3 - √5))
　= x^8 - 40 x^6 + 352 x^4 - 960 x^2 + 576
　といった、８次式になる。」
凛「ぎょえー、長い式！」
咲「でも、よく見ると + - が順番に、規則的に出てきているだけみたいだよ。」
Ａ「この場合も Ｑ(√２, √３, √５) = Ｑ( √２+√３+√５ ) だと見なして、
　√２+√３+√５ を答に含む方程式を考えるんだ。」
凛「次元、増えすぎだよ、、、たった３つなのに、掛け算で一気に８次元。。。」
咲「√を１つ付け加える度に、２、４，８・・・って２倍２倍に増えてゆくんですね。」
Ａ「“次元の増え方が掛け算になっている”、これは有用な結果だね。
　Ｑ → Ｑ(√２) で、ｘ２次元。
　Ｑ(√２) → Ｑ(√２,√３) で、さらにｘ２次元＝４次元。
　Ｑ(√２,√３) → Ｑ(√２,√３,√５) で、さらにｘ２次元＝８次元。」
凛「長いー式を見るより、１ステップでどれだけ次元が増えたかを見た方がわかりやすいね。」
Ａ「その、“１ステップでどれだけ次元が増えたか”ってことを“拡大次数”と言うんだ。
　こんな記号で書く。
　　[ Ｑ(√２) : Ｑ] = 2
　　[ Ｑ(√２,√３) : Ｑ(√２)] = 2
　　[ Ｑ(√２,√３,√５) : Ｑ(√２,√３) ] = 2 」
咲「それだと、
　　[ Ｑ(√２,√３,√５) : Ｑ] = 8
　ってことですね。」
Ａ「その通り。
　“次元の増え方が掛け算になっている”ということを、この記号で書くと、
　　[Ｋ：Ｌ][Ｌ：Ｆ] = [Ｋ：Ｆ]
　ってなるね。」
凛「記号にすると、いきなりレベルアップしたみたいだね。」

Ｇ「さて、√を付け加える感覚がつかめたところで、次は平方根以外のものも見てみよう。
　例えばＱに、三乗根 ³√2 を付け加えたＱ(³√2)は、何次元になるだろう？」
凛「なんか、３次元っぽい、今度こそ。」
Ｇ「当たり。でも、その理由は？」
凛「・・・直感。」（い、イジワル〜！）
Ｇ「よくわからなかったら、最小多項式に戻って考えてみること。
　³√2 の最小多項式は、x^3 - 2 だから３次式だ。
　なので、有理数Ｑからの拡大次元は３次元。
　　[ Ｑ(³√２) : Ｑ] = ３ 」
咲「でも、３次元だとしたら、いったいどんな軸が増えているのかしら。
　³√2 自身の他にも、もう１つあるということですよね。」
Ｇ「新たに増えるのは、 (³√2)^2 という軸だ。
　三乗根 ³√2 を付け加えると、体には同時に (³√2)^2 という数も含まれることになる。」
凛「うー、わかんないよー・・・」
Ａ「わからないときは、紙に書いてみようか。」

Ａ「この、体に属する数を見れば、整理が付くだろう。」
咲「なんかわかる気がするな。
　平方根は、a と b で二次元。
　立方根は、a と b と c で三次元。」
凛「そういうことか。立方根だと
　　(³√2) ^ 0
　　(³√2) ^ 1
　　(³√2) ^ 2
　って、３つの数が作れるから３次元になるんだ。
　平方根は、
　　√2 ^ 0
　　√2 ^ 1
　ってことで、２つだけだね。」
咲「そっかー、ってことは、四乗根だったら
　体に属する数 a + b ⁴√2 + c (⁴√2)^2 + c (⁴√2)^3
　の４次元。
　五乗根だったら
　体に属する数 a + b ⁵√2 + c (⁵√2)^2 + c (⁵√2)^3 + d (⁵√2)^4
　の５次元だね。」
凛「うわー、次元だらけだ。」

Ｇ「ここで驚いてはいけない、もっと次元だらけの空間もあるぞ。
　有理数に順番に代数的な数を付け加えていっても、実数には届かない。
　実数というのは、さしずめ無限次元空間といったところだ。」
凛「無限次元空間！」
って、有理数Ｑのまわりに、ウニみたいにびっしり次元軸の棘が生えているってことかしら？
。。。怖い考えになってしまった。
咲「・・・凛ちゃん、そんな深刻な顔しなくてもいいよ。」
凛「えっ、って、あたしそんな顔してた？」
Ａ「ははっ、心配しなくても大丈夫。
　方程式を代数的に解くという目的からすれば、有限次元だけを考えれば十分だ。」
凛「そ、そうだよね。３つか４つでいいんだよね。」
咲「たぶん五次方程式だったら５つまで、なのかな。」
Ａ「もう少し多くなるけど・・・まあ、そんなものだね。
　いままで平方根やベキ根のような、代数的な数の話ばかりだったけれど、
　実数の中にはπやｅのように、ベキ根では表しきれない超越数もあるんだ。
　例えばＱ(π)という体の次元を考えると、これも無限次元になってしまう。」
凛「も、もういいです。有限だけで大満足。」
私の頭の中で、ウニみたいに次元の棘を生やした体の空間が、ぐるぐる回りはじめた。
Ｇ「とりあえず今は、代数的な数の有限次元拡大だけが頭にあればいい。
　体の拡大には、代数拡大と、超越拡大の２つがある。
　有限次元の拡大は全て代数拡大。
　対して、超越拡大は全て無限次元だ。
　今後は代数拡大だけを考えてゆくことにしよう。」